本文是在2020年9月份,笔者参加全国大学生数学建模大赛时的参赛论文,最终获得吉林省二等奖的成绩,特此记录,欢迎各位大佬指导!
摘要:
针对问题一:利用回归分析方法建立其关系模型,进而转化为焊接件温度与时间的关系模型。其中,焊接件温度速率和温区温度与焊接件当前时刻温度之差的关系模型分别为:1-5区:??????????=0.0039(????−????)−0.211、6区:??????????=0.229(????−????)−1.8820、7区:??????????=0.2279(????−????)−3.3747、8-9区:??????????=0.0543(????−????)−0.3271;进而可得焊接区域温度变化规律模型分别为:1-5区:????=168.775−136.2858??−0.0339??;6区:????=186.781659−20.04165??−0.229??;7区:????=−39.64218955e3.33747t+220.1921895;8-9区: ????=−38.0660589e3.3747t+248.9760589。针对问题1中,当传送带温度为78cm/min时,各温区温度的变化情况以0.5s为间隔存放在result.csv中,其中小温区3、6、7中点及小温区8结束处焊接区域中心温度分别为:152.4℃、188.2697℃、212.8℃、239.8℃ 。
针对问题二,利用在问题一中建立的温度变化模型,在保证焊接件满足制程界限要求下,分别对各温区相应数据进行分析。由????=182−??−0.0339(339∗182−13124.11)339−6.2241887计算可知,在小温区1-5中,焊接件温度最高可升至175℃, 且焊接件温度从150升至175℃所需时间约为t=103s;由????=203−??−0.0229(229∗203+51177.32)229−8.5936073计算可知,在第6温区中,焊接件温度可从176℃最高升至194℃,其中由176℃升至190℃所需时间约为t=5s。由上述分析可知传送带速度?? ≥ 25cm/min。由“温度大于217℃的时间限定要求”40s-90s之间,根据????=237−??−0.2279??(2279∗237−445220.45)2279−14.8078104计算可知,在第7温区中,焊接件温度可从195℃最高升至222℃,其中由217℃升至222℃所需时间约为t=14s。由????=254−??−0.0543??(543∗254−117795.13)543−6.0239416计算可知,在小温区8-9内,峰值最高可达247℃,用时约40S。由上述分析可知传送带速度?? ≤ 155 cm/min。
针对问题三,通过对问题三的阅读,可知通过对炉温曲线超过217℃的峰值温度所覆盖的面积最小,通过限制处于217℃以上的时间处于最小即可,通过对问题二中的参数进行调整可以得出此要求小的最优炉温曲线,以及各温区的设定温度和传送带的过炉速度,并得出相应面积。
针对问题四,通过对问题四的阅读,可知在满足制程界限后,希望以峰值温度左右两侧的超过217℃的炉温曲线尽量对称,结合数学模型和逆向求解思维可得出调整后的最优炉温曲线,各温区的设定温度及传送带的过炉速度。
关键词:回归分析;回焊炉;温控
一、问题重述
为了生产集成电路板等电子产品,需要通过加热将安装有各种电子元件的印刷电路板放置在回焊炉中,将其焊接到电路板上。此时,让回焊炉的各部分保持工艺要求的温度,对产品至关重要。
已知项目中使用的回焊炉,其内部设置11个小温区,它们从功能上可分成四个大温区:预热区,恒温区,回流区,冷却区。每个小温区长度为30.5cm,相邻小温区之间有5cm 的间隙。内部还设有两个区域,分别为炉前区域和炉后区域且均为25cm。
问题 1 请对焊接区域的温度变化规律建立数学模型。假设传送带过炉速度 为 78 cm/min,各温区温度的设定值分别为 173º C(小温区 1~5)、198º C(小温 区 6)、230º C(小温区 7)和 257º C(小温区 8~9),请给出焊接区域中心的温 度变化情况,列出小温区 3、6、7 中点及小温区 8 结束处焊接区域中心的温度, 画出相应的炉温曲线,并将每隔0.5 s焊接区域中心的温度存放在提供的result.csv 中。
问题 2 假设各温区温度的设定值分别为 182ºC(小温区 1~5)、203ºC(小 温区 6)、237ºC(小温区 7)、254ºC(小温区 8~9),请确定允许的最大传送 带过炉速度。
问题 3 在焊接过程中,焊接区域中心的温度超过 217º C 的时间不宜过长, 峰值温度也不宜过高。理想的炉温曲线应使超过 217º C 到峰值温度所覆盖的面积 (图 2 中阴影部分)最小。请确定在此要求下的最优炉温曲线,以及各温区的设 定温度和传送带的过炉速度,并给出相应的面积
问题 4 在焊接过程中,除满足制程界限外,还希望以峰值温度为中心线的两侧超过 217º C 的炉温曲线应尽量对称(参见图 2)。请结合问题 3,进一步给出最优炉温曲线,以及各温区设定的温度及传送带过炉速度,并给出相应的指标值。
二、问题分析
本题主要是在回焊炉内部设置清晰及附件数据明确的前提下,研究项目成员通过对加热时,电子元件自动焊接到电路板上的这一过程的仿真问题,并在此基础上探求温度,速率,时间的变化规律。同时寻求团队的最佳协作策略。
针对问题一中的第一问,通过附件中某次实验数据给出的时间与温度的关系可得出元件初始温度,炉中元件温度与炉温的温度差,元件温度的增长速率。借助MATLAB与多元线性回归知识方可分别在小温区1-5、小温区6、小温区7、小温区8-9建立对应数学模型。建立模型后,假设问题一中初始温度变化率为0,
炉温与原件温度差已知,通过对应阶段数学模型方可递归求出不同位置元件的温度;最终根据所求数据画出相应炉温曲线。
当问题一中给定的过炉平均速度为78cm/min;1-5小温区的设定温度为173℃;6的小温区温度为198℃;7小温区的温度为230℃;8-9的小温区温度为257℃。
通过迭代关系可求出一系列——-数值后可以知道3,6,7中点与8结束外焊接区域中心温度的变化。
针对问题二,通过问题二中给出的制程界限,我们可以知道在电路板在回焊炉中需要满足的条件,根据问题中的所求的允许的最大传送带过炉速度。我们可知只要在满足制程界限的条件下使元件在回焊炉中所待时间越短越好。通过热力学知识和数学模型,从而求得最大过炉速度。
针对问题三,通过问题三中对炉温曲线超过217℃的峰值温度所覆盖的面积最小,我们可知通过限制217℃以上的时间处于最小值即可,同时分析每个不同的温区之间对峰值温度影响,同时将峰值温度尽快达到制程界限的240℃-250℃之间达到最快的节省时间的目的,从而 确定最优炉温曲线,各温区的设定温度,传送带的过炉速度,并且求出相应的面积
针对问题四,在根据问题三的基础上获得最优炉温曲线后,尽量使217℃左右两侧炉温曲线尽量对称通过数学模型的温度分布曲线,反推出各温区的设定温度及传送带过炉速度。
三、模型假设
1.假设小温区之间的间隔温度不做特殊温度控制,温度与相邻温区的温度有关。
四、符号说明
Vu 温度上升速率
Ti 当前时刻温度
ti 当前时刻
Tc 元件与炉温温差
Ts 炉内设定温度
Tt 炉内元件温度
Kn 常数
五、模型的建立与求解
5.1.问题一的模型的建立与求解
5.1.1问题一模型的分析
问题一可分为两个小问,即1.列出小温区3、6、7中点及小温区8结束处焊接区域中心的温度,2. 画出相应的炉温曲线,并将每隔0.5 s焊接区域中心的温度存放在提供的result.csv中。而将炉温曲线画出后可通过计算焊接件在通过小温区3、6、7中点的时间从而在炉温曲线上找到相应的温度,因此第一问的解决重点应放在焊接件的炉温曲线变化情况上。
焊接件在炉前温区时温度为25℃,在进入小温区1时开始升温,在温度达到30℃时温度传感器开始工作,其焊接件温度在温区内将持续上升,但上升速率会逐渐下降。由于温区间隙受温区内温度的影响,因此间隙温度取两相邻温区温度的平均值。相同温度的温区间隙不需特殊考虑。因此可将回焊炉按温度划分为以下几个区域:1—5区、5,6区间隙、6区、6,7区间隙、7区、7,8区间隙、8-9区及炉前炉后区。由于焊接件在炉前炉后区温度降到30℃一下,温度传感器不工作,可不做计算。
5.1.2问题一模型的建立
由于已知焊接件的初始温度,想求出在焊炉中某一时刻的温度即需要温度增长速率,用温度增长速率乘以所用的时间即为该段时间内温度增加量,再加上初始温度可得到当前时刻的温度,对于当前时刻的温度Ti,前一时刻温度Ti-1。当时时间ti,前一刻时间ti-1有:
????=????−????−1????−????−1 (1)
由附件给出的温度变化情况来看,随着温度的不断升高,温度的上升速度越来越慢,由此可以得出温度增长速率跟炉温和焊接件的温差有关。以炉温与焊接件的温差为横坐标,温度增长速率为纵坐标绘制温度增长速率的变化曲线(如图1)。

我们可将上图曲线近似看作抛物线,假设温差与温度增长的速率成二次函数关系;设炉温为Ts,炉内原件温度为Tt,并建立方程:
????=??1(????−????)2+??2(????−????)+??3 (2)
由于
????=????−????−1????−????−1=?????????? (3)
因此可得最终方程:
??????????=??1(????−????)2+??2(????−????)+??3 (4)
由于不同温区温度不同,因此在计算时需对不同温度的温区建立对应的微分方程,并在已有数据基础上进行计算,得出微分方程中各部分的数据。
据题,炉温已知,利用公式(1)可计算出每个时间段内温度的变化率,时间间隔为0.5s;设Tc为炉内温度与焊接件温度的差值,即公式中的????−????。
根据题目提供的附件,可通过(2)式与(5)计算出, ????与????。(如图2-5所示)
????=????−???? ( 5 )




5.1.3问题一模型的求解
由于不同区域的炉温不同,我们需要对不同温区(即预热区1~5、恒温区6、回流区7,回流区 8~9、冷却区10~11)建立对应微分方程依次求解;在分别对温度相同的温区建立微分方程时,只需更改Ts的大小即可。
以1-5温区为例,由多元线性回归知识,借助matlab编程(如代码一)可得:K1、K2、K3分别为:-0.211、-0.0001、0.0339,因-0.0001数值过小,故舍去K2,得最终模型为:
??????????=0.0039(????−????)−0.211 (6)
再根据代码二,解出微分方程:
????=????−??−0.0339(339????−13124.11)339−6.2241887 (7)
????=168.775−136.2858??−0.0339?? (8)
由此可以得出焊接件在1-5温区内的温度变化曲线:(如图6;见代码一)

同1-5温区的计算过程,通过matlab编程可得到其余温区的模型及温度变化曲线:
11
6区:
??????????=0.229(????−????)−1.8820 (9)
????=????−??−0.0229(229????+51177.32)229−8.5936073 (10)
????=186.781659−20.04165??−0.229?? (11)

7区: ??????????=0.2279(????−????)−3.3747 (12)
????=????−??−0.2279??(2279????−445220.45)2279−14.8078104 (13)
????=−39.64218955e3.33747t+220.1921895 (14)

8-9区: ??????????=0.0543(????−????)−0.3271 (15) ????=????−??−0.0543??(543????−117795.13)543−6.0239416 (16) ????=−38.0660589e3.3747t+248.9760589 (17)

将不同温度下的????进行整合,并以0.5为步长,使用matlab建立温度-时间总曲线。(代码二)

5.1.4模型求解
由上述数学模型可得,在炉温为173℃时,可通过matlab编程得到相应的炉温变化曲线。(如图11;代码三)
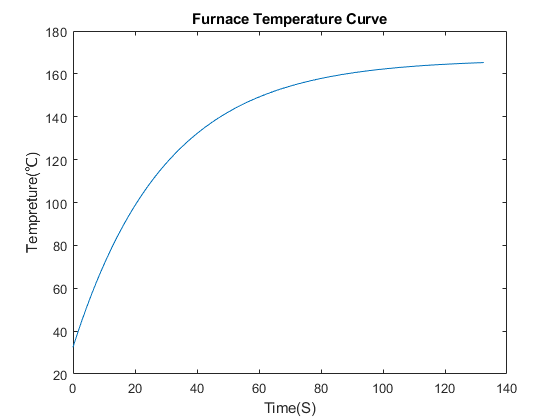
由于焊接件是以78 cm/min的速度匀速运行,达到3区的时间为??=????????=86.251.3=66.3461??,在温度变化曲线上可找到对应的温度为152.4℃
同理在小温区6,198℃下的温度变化曲线为(如图12):
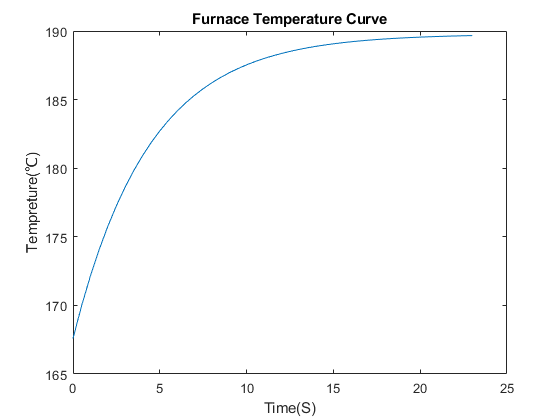
焊接件到达小温区6的时间为t=148.269,对应的温度为188.2697℃
在7区237℃下的温度变化曲线为:
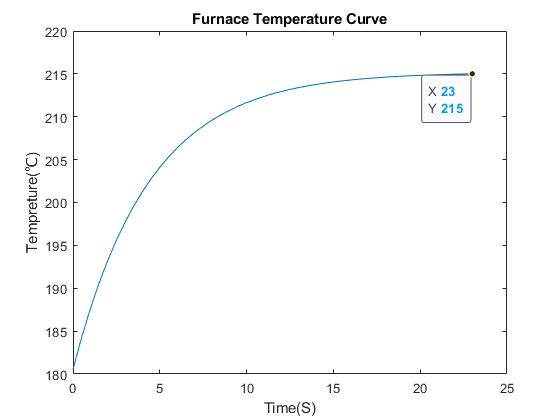
焊接件到达7区中间的时间t=175.5769,对应的温度为212.8℃
在8区255℃下的温度变化曲线为:
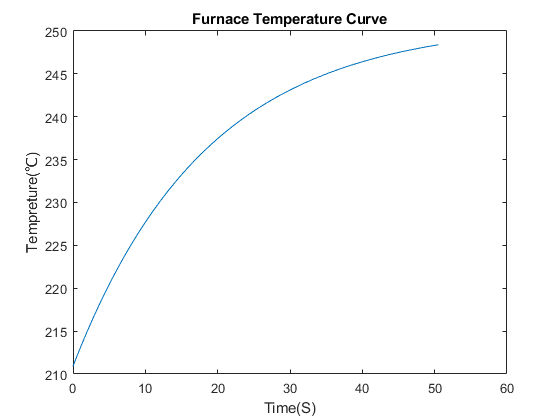
焊接件到达8区末的时间为t=365.384,对应的温度为239.8℃
将不同炉温所建立的模型中找出不同时间相对应的温度数据,汇总成以下表格(图16)
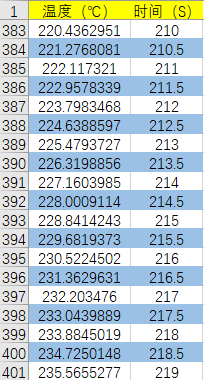

根据表格中的数据,使用matlab编程(代码四)即可得到焊接件在题目要求下的温度变化曲线:(数据如图17)
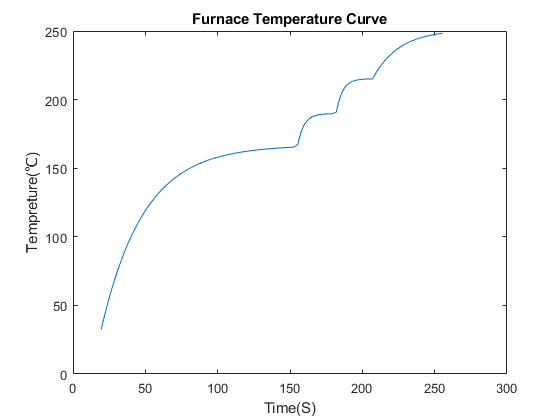

5.2问题二模型建立:
针对问题二,通过文中给出的制程界限,我们可以知道在电路板在回焊炉中需要满足的条件,根据问题中的所求的允许的最大传送带过炉速度。我们可知只要在满足制程界限的条件下使元件在回焊炉中所待时间越短越好。通过热力学知识和数学模型,从而求得最大过炉速度。
由问题一中的公式(7): ????=????−??−0.0339(339????−13124.11)339−6.2241887
可知,当Ts=182℃时,有 ????=182−??−0.0339(339∗182−13124.11)339−6.2241887 (18)
根据制程界限表中关于“温度上升过程中在150-190℃之间的时间限定”要求,由公式(18)计算可知,在小温区1-5中,焊接件温度最高可升至175℃, 且焊接件温度从150升至175℃所需时间约为t=103s,见代码
由问题一中公式(9)
????=????−??−0.0229(229????+51177.32)229−8.5936073
可知当Ts=203℃时,有
????=203−??−0.0229(229∗203+51177.32)229−8.5936073 (19)
由公式(19)计算可知,在第6温区中,焊接件温度可从176℃最高升至194℃,其中由176℃升至190℃所需时间约为t=5s。
由制程界限表中温度上升过程中在150-190℃之间的时间限定要求为60s-120s之间,而由上述计算可知,1-5区和6区共花费时间约为108s;所以,1-5区与6区间隔区通过时间最多为12 S;设传送带速度为v,则有 5? ≤12,即?? ≥ 25cm/min。
根据制程界限表中关于“温度大于217℃的时间限定要求”40s-90s之间,由问题一中公式(13)
????=????−??−0.2279??(2279????−445220.45)2279−14.8078104
可知当Ts=237℃时,有
????=237−??−0.2279??(2279∗237−445220.45)2279−14.8078104 (20)
由公式(20)计算可知,在第7温区中,焊接件温度可从195℃最高升至222℃,其中由217℃升至222℃所需时间约为t=14s。
由问题一中的公式(15):
????=????−??−0.0543??(543????−117795.13)543−6.0239416
可知当Ts=254℃时,有
????=254−??−0.0543??(543∗254−117795.13)543−6.0239416 (21)
由公式(21)计算可知,在小温区8-9内,峰值最高可达247℃,用时约40S,设传送带速度为v,则有 54??≤3×30.5+10,即?? ≤ 155 cm/min。
5.3问题三模型建立
根据问题一中建立的温度变化曲线模型,过217℃对217℃到峰值温度所覆盖的面积求最小值,即对函数:
??????????=0.0039(????−????)−0.211 (22)
在焊接件中心温度到达217℃时,所对应的时间,及达到峰值温度所对应的时间,在这两个时间内通过模型求积分,得到关于Ts的方程,对方程求解计算Ts的最小值。将最小值代入所求积分计算出相应的面积[1]。此时再将Ts带回模型中利用MATLAB此时相对应的温度变化曲线。
5.4问题四的模型建立
由问题三计算结果可知回流区的炉温是NNN,由问题一得出的冷却区(10-11)的数学模型在焊接件中心温度到达217℃时值温度所对应的时间,在这两个时间内通过模型求积分。计算方法同问题三,得出冷却区的设定炉温,利用MATLAB画出冷却区的温度变化曲线。
六、评价与改进
优点:
- 运用已知附件的数据,我们能考虑到不同炉温下,温度变化速率的不同,更加贴近实际,
- 数学模型的建立比较简单,专业程度不高,便于理解。
缺点: - 没能考虑不同温区间隔的温度,模型不够精确。
- 实际情况中不该把焊接件考虑成质点,忽略了焊接件不同位置的温度变化情况
改进:
1.查阅更多资料,确定不同温区间间隔的温度,细化焊接件的温度变化情况,进一步优化模型。
七、参考文献
[1]李岩,赵立博,张伟, 等.对回流焊炉温度设定的分析与优化[J].船电技术,2010,30(7):44-46. DOI:10.3969/j.issn.1003-4862.2010.07.012.
附录:
代码一:
%Section 1-5
clc;
clear;
y= xlsread(‘zuixin.xlsx’,’D7:D302′); %Vu
x= xlsread(‘zuixin.xlsx’,’E7:E302′); %Tc
X= [ones(size(y)),x.^2 x];
%analys
[b,bint,r,rint.stats] = regress(y,X);
syms x y Z;
y=dsolve(‘Dy+0.0339y=0.0339Z-0.211′,’y(0)=32.49′,’x’)
simplify(y);
x=0:0.5:147.5;
y=168.775-136.2858.exp(-0.0339x);
plot(x,y)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)
%Section 6
clc;
clear;
y= xlsread(‘zuixin.xlsx’,’D312:D363′); %Vu
x= xlsread(‘zuixin.xlsx’,’E312:E363′); %Tc
X= [ones(size(y)),x.^2 x];
%analys
[b,bint,r,rint.stats] = regress(y,X);
syms x y Z;
y=dsolve(‘Dy-0.229y=0.229Z-1.8820′,’y(0)=242.28′,’x’)
simplify(y);
x=0:0.5:25.5;
y=186.781659-20.04165.exp(-0.229x);
plot(x,y)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)
%Section 7
clc;
clear;
y= xlsread(‘zuixin.xlsx’,’D373:D424′); %Vu
x= xlsread(‘zuixin.xlsx’,’E373:E424′); %Tc
X= [ones(size(y)),x.^2 x];
%analys
[b,bint,r,rint.stats] = regress(y,X);
syms x y Z;
y=dsolve(‘Dy+0.2279y=0.2279Z-3.3747′,’y(0)=180.55′,’x’)
simplify(y);
x=0:0.5:26;
y=220.1921895-39.64218955.exp(-0.2279x);
plot(x,y)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)
%Section 8-9
clc;
clear;
y= xlsread(‘zuixin.xlsx’,’D433:D546′); %Vu
x= xlsread(‘zuixin.xlsx’,’E433:E546′); %Tc
X= [ones(size(y)),x.^2 x];
%analys
[b,bint,r,rint.stats] = regress(y,X);
syms x y Z;
y=dsolve(‘Dy+0.0543y=0.0543Z-0.3271′,’y(0)=210.91′,’x’)
simplify(y);
x=0:0.5:57;
y=248.9760589-38.0660589.exp(-0.0543x);
plot(x,y)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)
%Section 10-11
clc;
clear;
y= xlsread(‘zuixin.xlsx’,’D555:D667′); %Vu
x= xlsread(‘zuixin.xlsx’,’E555:E667′); %Tc
X= [ones(size(y)),x.^2 x];
%analys
[b,bint,r,rint.stats] = regress(y,X);
syms x y;
y=dsolve(‘Dy-0.2624y=27.6433′,’y(0)=242.28′,’x’) simplify(y); x=0:0.5:56.5; y=105.347942+347.627942.exp(0.2624x); plot(x,y) xlabel(‘Time(S)’) ylabel(‘Tempreture(℃)’) title(‘Furnace Temperature Curve’) 代码二: T = xlsread(‘sum.xlsx’,’A1:A908′) t = xlsread(‘sum.xlsx’,’B1:B908′) plot(t,T) xlabel(‘Time(S)’) ylabel(‘Tempreture(℃)’) title(‘Furnace Temperature Curve’) 代码三: %Section 1-5 clc; clear; x=0:0.5:132.5; y=173-(exp(-(339x)/10000)(339173 – 1312411/100))/339-2110/339;
plot(x,y)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)
%Section 6
x=0:0.5:23;
y=198 – (exp(-(229x)/1000)(229198 – 4026011/100))/229 – 1882/229; plot(x,y) xlabel(‘Time(S)’) ylabel(‘Tempreture(℃)’) title(‘Furnace Temperature Curve’) %Section 7 x=0:0.5:23; y=230 – (exp(-(2279x)/10000)(2279230 – 8904409/20))/2279 – 33747/2279;
plot(x,y)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)
%Section 8-9
x=0:0.5:50.5;
y=257 – (exp(-(543x)/10000)(543*257 – 11779513/100))/543 – 3271/543;
plot(x,y)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)
代码四:
T = xlsread(‘sum1n.xlsx’,’A1:A473′);
t = xlsread(‘sum1n.xlsx’,’B1:B473′);
plot(t,T)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)
x=0:0.5:23;
y=198 – (exp(-(229x)/1000)(229198 – 4026011/100))/229 – 1882/229; plot(x,y) xlabel(‘Time(S)’) ylabel(‘Tempreture(℃)’) title(‘Furnace Temperature Curve’) %Section 7 x=0:0.5:23; y=230 – (exp(-(2279x)/10000)(2279230 – 8904409/20))/2279 – 33747/2279;
plot(x,y)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)
%Section 8-9
x=0:0.5:50.5;
y=257 – (exp(-(543x)/10000)(543*257 – 11779513/100))/543 – 3271/543;
plot(x,y)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)
代码四:
T = xlsread(‘sum1n.xlsx’,’A1:A473′);
t = xlsread(‘sum1n.xlsx’,’B1:B473′);
plot(t,T)
xlabel(‘Time(S)’)
ylabel(‘Tempreture(℃)’)
title(‘Furnace Temperature Curve’)

